In order to perform this, we first choose a clean grayscale image containing some texts within. The chosen image is shown in Figure 1. This image was then degraded by adding a Gaussian noise with it. The discussion about this noise model has been stated in the previous activity.
To perform the restoration, a simple model adapted from the handout [1] is displayed in figure 2. The image is degraded by convolving the degradation function h(x,y) with the image f(x,y) and adding the Gaussian noise
 (x,y). Note that this is in spatial domain. In order to transform this to the frequency domain, we take the Fourier transform of the terms and apply equation 2 in the handout, given by:
(x,y). Note that this is in spatial domain. In order to transform this to the frequency domain, we take the Fourier transform of the terms and apply equation 2 in the handout, given by:where capital letters correspond to the Fourier transform of the functions.

Figure 1. Clean image

Figure 2. Model of image degradation and restoration.
If we assume that the image is blurred by a linear motion between the sensor and the image during the acquisition, the image then undergoes a planar displacement in the x and y direction which varies through time t. In order to obtain to total exposure at any point of the recording medium, the integral of the instantaneous exposure is taken over the time interval for which the imaging shutter is opened. And if the opening and closing of the shutter occurs instantaneously, we can isolate the image motion and arrive at the blurred image using the formula:
where T is the exposure time. This can also be expressed in the frequency domain which is equivalent to:
The degradation function H is estimated using the following expression
Note that the variables a and b correspond to the total distance from which the image is displaced in the x and y direction.
In order to employ Weiner filtering, we treat the the image and the noise as random processes and try to estimate such that its mean square error with the original image f is small. This is performed mathematically by using the the equations:
such that its mean square error with the original image f is small. This is performed mathematically by using the the equations:
Alternatively, the expression for F above can be approximated by the equation:
where K is a constant. This is particularly used when we are dealing with spectral white noise such that the spectrum is constant.
By varying the parameters a b and T, we apply Gaussian noise and degrade the image. The results for this degradation process are shown in Figure2. Using the last two expressions for , we try to restore these blurred images and the are shown in Figures 3 and 4.
, we try to restore these blurred images and the are shown in Figures 3 and 4.
where T is the exposure time. This can also be expressed in the frequency domain which is equivalent to:
The degradation function H is estimated using the following expression
Note that the variables a and b correspond to the total distance from which the image is displaced in the x and y direction.
In order to employ Weiner filtering, we treat the the image and the noise as random processes and try to estimate
 such that its mean square error with the original image f is small. This is performed mathematically by using the the equations:
such that its mean square error with the original image f is small. This is performed mathematically by using the the equations:Alternatively, the expression for F above can be approximated by the equation:
where K is a constant. This is particularly used when we are dealing with spectral white noise such that the spectrum is constant.
By varying the parameters a b and T, we apply Gaussian noise and degrade the image. The results for this degradation process are shown in Figure2. Using the last two expressions for
 , we try to restore these blurred images and the are shown in Figures 3 and 4.
, we try to restore these blurred images and the are shown in Figures 3 and 4.



Figure 2. Degradation of the image using different values of a, b, and T
Upon increasing the values of a and b, image becomes more blurry. This is reasonable since upon increasing the distance for which the image is displaced along the x and y axis with respect to the recording medium, lesser the information about the image can be generated. And it is seen that at a=b= 0.1, most of the information regarding the image is lost.




Figure 3. Restoration of the image using Weiner Filtering
From the figure above, the quality of the degraded image was improved, although it was not totally recovered. And comparing the images before and after applying Weiner flitering, we can observe that some of the information regarding the original image were restored. However, among the four sets of images, the restoration for a=b=0.1 is poorest.




Figure 4. Restoration of the image using Weiner Filtering equation 2 for different K, a, b, and T.
After using the second equation for the Weiner filtering and using different values for K (0.005-0.01 with 0.001 interval), restoration of some information in the image was done. However, if we compared the result with Figure 3, it can be seen that richer image quality is obtained in the first expression. And after varying K, no significant difference was observed.
In this activity, I was able to restore the degraded image corrupted with a degradation function and a Gaussian noise model so I am giving myself a grade of 10.
Reference:
" Restoration of blurred images", Activity 18 Handout, Applied Physics 186.
In this activity, I was able to restore the degraded image corrupted with a degradation function and a Gaussian noise model so I am giving myself a grade of 10.
Reference:
" Restoration of blurred images", Activity 18 Handout, Applied Physics 186.

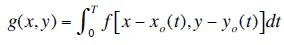





No comments:
Post a Comment