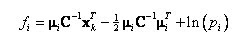Activity 16 Neural Networks

In this activity, pattern recognition is employed by using neural networks...

Neural network is a computational model that mimics the behavior of the neurons in the brain [1]. It is more advantageous than linear discriminant analysis because it also considers nonlinear systems. It is able to model nonlinear functions containing large variables which make it useful to several applications such as detection of medical phenomena, stock market prediction, credit assignment, monitoring the condition of machinery, and engine machinery [2].

To implement neural network model, I considered 10 sample objects consisting of blue and red dinosaurs as shown in Figure 1. Four feature vectors, namely the red chromaticity value, green chromaticity value, blue chromaticity value, and area were utilized for classification. The area values of the objects were normalized with respect to the highest value so the feature vectors can be correlated with one another. The first five rows of each column correspond to the blue dinosaurs while the last five rows describe the feature vectors of the red dinosaurs. The matrix below shows the arrangement of the training set and the feature vectors. The first, second, third, and fourth columns are designated to red chromaticity value, green chromaticity value, blue chromaticity value, and normalized area, respectively.

Figure 1. Image used for neural network

For this case, I chose the red dinosaurs as my desired class, so the desired output is written such that the class of blue dinosaurs is set to 0 and red dinosaurs to 1. By adopting the code of Mr. Jeric Tugaff for neural network posted in Mr. Cole’s blog [3], the results shown in Figure 2 and 3 were obtained. The number of iterations (T) and learning rate (LR) were varied and their effects to the accuracy of recognition were observed. The values for T were changed from 100 to 500 with an increment of 100, and it was found that more accurate pattern recognition is acquired for higher T, that is, blue-colored dinosaurs resulted to values nearest to 0 and red dinosaurs nearest to 1. Thus, T=500 yield the most accurate pattern recognition ability from the range chosen, and it was utilized for determining the effect of LR to the accuracy of recognition (see Figure 3). LR was varied from 0.1 to 2 and it can be observed that more accurate pattern recognition is attained as the LR is increased. From the range of LR values, LR=2 yielded the highest accuracy for pattern recognition by having values of red dinosaurs closest to 1 and blue dinosaurs closest to 0. However, it cannot be concluded that T=500 and LR=2 are the optimized parameters for acquiring the most accurate pattern recognition ability since we can still extend the range and seek for more combination of LR and T.

Figure 2. Results obtained for different T


Figure 3. Results obtained for different LR

Since I was able to meet the objective of the activity, I give myself a grade of 10. I would like to acknowledge Master and Orly for helping me improve my results.

References:

1. "Neural Networks", Activity 16 Manual.

2. "Neural Networks", Statsoft Inc., http://www.statsoft.com/textbook/stneunet.html#apps.

3. http://cole-ap186.blogspot.com/

Activity 15 Probabilistic Classification

Pattern recognition was performed in the previous activity using the Euclidean distance. Now, we are going to employ Linear Discriminant Analysis (LDA) for classifying members of a certain group. The image from the previous activity are reused for this purpose and is shown in Figure 1. LDA shows that groups can be separated by a linear combination of features that are used to describe the members.

Figure1. Image used for pattern recognition using LDA

Using the object features, the members are assigned to the group with highest conditional probability. This is known as Baye's rule, which helps minimize the total error of classification (TEC). Mathematically, it is expressed as the object belong to group i where

Thus, the probability that the member belongs to group i given a set of data x is determined.

To implement LDA, we form a matrix x consisting of rows of objects and columns of features. For this particular activity, I used the same objects (blue and red dinaosaurs) and same features as the previous activity, that is, r_values and area. From this matrix, the two classes of objects are separated (x1 and x2) with their corresponding features. To visualize this, refer to the equation below.

From x1 and x2, the mean features u1 and u1, and global mean vector are determined which are used to get the mean corrected data x10 and x2o. From these values, the pooled covariance matrix are calculated using the equation

where g is the number of groups ci(r,s) is the covariance of each group. Finally, the discriminant function is solved using the following formula:

The selection of an object to a particular group is by choosing the Fi of the class with higher value. Here, F1 correspond to the class of red dinosaurs while F2 to the blue dinosaurs. Table 1 shows the result after performing LDA.

Table 1. Results obtained after applying LDA

The percentage of correct prediction of the classification is 100%.
For this activity, I am able to apply LDA to classify objects belonging to a certain class. Since I met the objective, I give myself a grade of 10.

References:
http://people.revoledu.com/kardi/tutorial/LDA/
http://www.craftkitsandsupplies.com/images/Foam_Shapes/Foam_Dinosaur_Shapes.jpg

Activity 14 Pattern Recognition

In image processing, it is important to distinguish sets of classes which share common features such as size, shape, color, and others. These sets of features are known as pattern and the process of determining the set of features that will enable the separation of a set into classes in called pattern recognition. In this activity, our task is to apply pattern recognition in images. Careful choice of the class features is important in this activity since it helps simplify our problem.

Mathematically, patterns maybe arranged into ordered sets such as feature vectors. If we let ωj, where j=1, 2, 3, …, W be a set of classes and W the total number of classes, we can define a representative of class ωj such that its mean feature vector is:

where xj is the set of all feature vectors in class ωj and Nj is the number of sampls in ωj. The class membership is determined by classifying an unknown feature vector x to the class whose mean is nearest to it. The Euclidean distance is used for this case and is equal to:

where is the ||y|| = (y^Ty)^1/2 Euclidean norm [1].

The image [2] chosen for this activity is shown in Figure 1. As seen from the figure, the members of the entire class are dinosaurs of different types. From these dinosaurs, two classes are chosen and are shown in Figure 2. The figure consists of 5 blue dinosaurs and 5 red dinosaurs. The first three pictures of each row served as the training sets while the last two are the test objects. The classes are differentiated from each other in terms of color and area. For the first feature in our pattern recognition, the RGB values of each training sets are determined. Then, the normalized chromaticity for red (denoted as r_value) and the mean r_value for the two classes are calculated. For the second feature, i.e. area, the training objects are first converted to binary images (with proper thresholding). Using the code for area calculation in activity 2, the area of each training object and the mean area for each class are obtained. Table 1 shows a summary of the r_value and area for each training object.

Figure 1. Image used for pattern recognition [2]

Figure 2. Selected classes from image



Table 1. r_value and area of the training set.

To clearly see the separation between the two classes using the features selected, the r_values for differentarea of each training object are plotted and is shown in Figure 3. Notice that the separation between the classes is large enough to classify the objects. This signifies that the chosen features are reliable for pattern recognition.

Figure 3. Plot of r_values versus area of the training objects

For the test objects, the r_value and area are also calculated. Using Euclidean distance, test objects are classified as to what class they belong. The computed values and the classifications are shown in Table 2 and the plot of r_values vs. area is shown in Figure 4.

Table 2. Tabulated r_value and area of the test objects and their classifications

Figure 4. Plot of r_values vs. area of the test objects

From this activity, I was able to perform pattern recognition by supplying the right feature of each class and predicting the class from which the test objects belong. I would like to thank Kaye Vergel for that good discussion.

Since I am able to meet the objective of the activity, I give myself a grade of 10.

References:

1. Activity manual for Pattern recognition

2. http://www.craftkitsandsupplies.com/images/Foam_Shapes/Foam_Dinosaur_Shapes.jpg